- 搬题人:
- DNA 匹配 2:Qingyu
- 情报传递 3:Qingyu
- 别急 2:Qingyu
- 旅程:flower
- 染色:Qingyu
- 运算符 2:feecle6418
- 匹配求和:Qingyu
- 组题人:Qingyu
- 验题人:feecle6418, flower, gyh20, test12345
UOJ 缺投!
DNA 匹配 2(50 Points)
来源:
- infO(1) Cup 2017 National Round. Problem 2, DNA
链接:https://qoj.ac/contest/998/problem/4713
算法 1
题目好难啊,不太会做,干脆输出随机数吧!
期望得分 $1 \sim 2$ 分。
算法 2
我们接着输出随机数,由于是 bitand,所以我们考虑随机的时候让每个数的 popcount 大一些,例如要求每个数 popcount 至少为 $14$。
期望得分 $10 \sim 30$ 分。
算法 3
考虑将 $2000$ 个数分成两组 $A, B$,每组包含 $1000$ 个数。将第一组的二进制表示下 $0 \sim 9$ 位钦定为 $1$,$10 \sim 19$ 位设为随机数。将第一组的二进制表示下 $0 \sim 9$ 位设为随机数,$10 \sim 19$ 位钦定为 $1$。并假设任意两个数两两不同。
此时,注意到任取一对 $x \in A, y\in B$,$x \operatorname{and} y$ 恰好包含了 $y$ 的前 $10$ 位与 $x$ 的后 $10$ 位,这至少包含了 $1000\times 1000 = 10^6$ 种不同的结果。
期望得分 $50$ 分(满分)。
情报传递 3(50 Points)
来源:
- ByteDance-Moscow Workshops Camp 2022. Shuffle Contest. Problem M, Multiple Communications
链接:https://qoj.ac/contest/997/problem/4675
算法 1
题目好难啊,不太会做,那就干脆把所有数都发过去吧!
需要 $NL$ 个 bit,可以通过子任务 1,获得 $5$ 分。
算法 2
如果 $x, y$ 均均匀独立随机生成,那么其前 $\ell$ 位相等的概率为 $2^{-\ell}$。因此,对于子任务 $3$,在数据随机的情形下,我们可以给每个串直接截取前 $30$ 位发送过去,并在询问时只使用 $C$ 的前 $30$ 位。
需要使用 $30N$ 个 bit,可以通过子任务 1 与子任务 3,获得 $10$ 分。
算法 3
算法 2 存在的问题是,我们可以刻意钦定一些位,使得每个串在这些位上均相等。为了避免攻击,我们可以给每个位 $i$ 附上一个 $[0,2^{30})$ 内的随机权值 $w_i$。根据 Schwartz–Zippel lemma,发生碰撞的概率即为 $\Pr[P(r_1,r_2,\ldots,r_n)=0]\leq\frac{d}{|S|}$。
需要使用 $30N$ 个 bit,期望得分 $50$ 分(满分)。
别急 2(75 Points)
来源:
- ByteDance-Moscow Workshops Camp 2022. Shuffle Contest. Problem B, Broken Connection
链接:https://qoj.ac/contest/997/problem/4664
观察
注意到我们发送过去后顺序会被随机打乱,因此我们可以认为我们只能传递每种数的数量。
问题可以转化为我们可以发送 $10$ 个非负整数变量 $x_0,x_1,\cdots, x_9$,且需要保证 $\sum_{i=0}^9 x_i \le L$。
算法 1
注意到我们要传递一个 $10$ 位 $10$ 进制数,我们不妨考虑用 $x_i$ 来表示第 $i+1$ 位的值。这样在最坏情况下需要使用长为 $100$ 的字符串,得分 $7.5$ 分。
在此基础上可以进行一些常数优化,例如给每一位随机一个排列 $p_{0\cdots 9}$,转而使用 $p_i$ 来表示,这样期望情况下每一位只会用到长为一半的字符串,可以获得更多的分数。
算法 2
注意到对于方程 $x_1+\cdots+x_n = m$,我们可以使用隔板法来计数其非负整数解的数量 $f(n,m) = \binom{m+n-1}{n-1}$。因此,我们可以快速的求出一个局面的字典序。注意到当 $L=50$ 时,$\binom{50+10-1}{10-1} = 12565671261 > 10^{10}$,因此我们直接使用解的字典序来编码 $X$ 即可。
期望得分 $75$ 分(满分)。
旅程(75 Points)
来源:
- Natjecanje timova studenata informatičara hrvatskih sveučilišta 2012. Problem G. Restorani
链接:https://qoj.ac/contest/433/problem/4852
算法 1
可以把题意中 $u$ 对 $v$ 喜欢,建成 $u$ 到 $v$ 的有向边。那么 $u$ 推荐 $v$ 就等价于,可以从 $u$ 走到 $v$。
先缩点后,对于每个scc考虑决策。
- 不经过这个 scc,代价是 0。
- 经过 $k$ 个此 scc 的点,其中 $1$ 个点的代价 $y_u$,剩下 $k-1$ 个点的代价是 $x_u$。
因此考虑预处理 $f_{u,i}$ 表示在第 $u$ 个 scc 经过 $i$ 个点的最代价。
令 $g_{u,i}$ 表示从第 $u$ 个 scc 开始走,经过 $i$ 个点的最小代价,转移是枚举 $u$ 的出边,和 $u$ 里走过了多少点,时间复杂度 $O(n^3)$
染色(75 Points)
来源:
- QOJ 141(https://qoj.ac/problem/141 )
本题修改自 Hong Kong Olympiad in Informatics 2014 Senior Group(香港電腦奧林匹克 2014 高級組)中的 Dividing the Cities(城市分配)一题。
算法 1
题目好难啊,不太会做,直接把整个方案给发送过去吧。
每个颜色需要占用 $3$ 个 bit,共需 $3N$ 个 bit,期望得分 $2$ 分。
算法 2A
如果 Bob 自力更生,自己寻找染色方案,那么是非常困难的。但是对一张图 $2$ - 染色非常简单:我们只需要 DFS 一遍即可。
我们不妨将颜色两两配对,对于颜色 $c$ 我们发送颜色 $\left\lfloor c/2\right \rfloor$。此时,我们需要将每一种颜色 $c'$,区分为 $2c'$ 与 $2c'+1$。这相当于我们要将这种颜色的点进行 $2$ - 染色,我们只需要 DFS 整张图即可线性完成。
这样,每个颜色只需要占用 $2$ 个 bit,共需 $2N$ 个 bit,期望得分 $24.85$ 分。
算法 2B
我们考虑另一个角度。如果这张图中,某个点的度数小于 $8$,那么我们可以直接删去这个点:将其余部分的染色方案复原后,他至多只有 $7$ 个邻居,因此总有一种颜色它可以直接使用。
这样,我们可以不断地删去图中度数小于 $8$ 的点,直到所有点的度数都至少为 $8$。由于一条边至多对度数之和贡献 $2$,因此剩余的点数不可能超过 $M/4$ 个。
这样,我们只需要发送 $M/4$ 个点的信息,共需 $3M/4$ 个 bit,期望得分 $30.92$ 分。
算法 3
同时使用算法 2A 与算法 2B,共需 $M/2$ 个 bit,期望得分 $75$ 分(满分)。
运算符 2(125 Points)
来源:
- Petrozavodsk Winter 2021. Day 8. Belarusian SU Contest, Yandex Cup. Problem A. Belarusian State University
- XXI Open Cup named after E.V. Pankratiev, Grand Prix of Belarus. Problem A. Belarusian State University
链接:https://qoj.ac/contest/536/problem/1083
算法 1
可以发现,二元 01 运算一共只有以下几种:
- 恒 0 / 恒 1。这时可以通过重新对下标赋值,将其转为 AND 运算。
- $f(x,y)=x$ 或 $f(x,y)=y$,或 $f(x,y)$ 等于 $x$ 或 $y$ 取反。这时可以通过重新对无关一边的下标赋值 1,将其转为 AND 运算。
- 等价于,或把 $x$ 取反后等价,或把 $y$ 取反后等价,或均取反后等价 AND/XOR。
进行适当操作后,直接在每位上分别运用通常的 AND/XOR 卷积的处理方式即可。可以证明,AND 与 XOR 运算在每一位上不会互相干扰。
时间复杂度 $O(2^nn)$。
匹配求和(200 Points)
来源:
- Petrozavodsk Winter 2020. Day 9. Yuhao Du Contest 7. Problem F. Fast as Ryser
- XX Open Cup named after E.V. Pankratiev, Grand Prix of Zhejiang. Problem F. Fast as Ryser
链接:https://qoj.ac/contest/449/problem/2068
算法 1
设 $E_0 = \{ (1, 2), (3, 4), \cdots \}$,则注意到对任意 $E' \subseteq E$,$E'$ 是匹配当且仅当 $E' \cup E_0$ 是若干环与链的并。
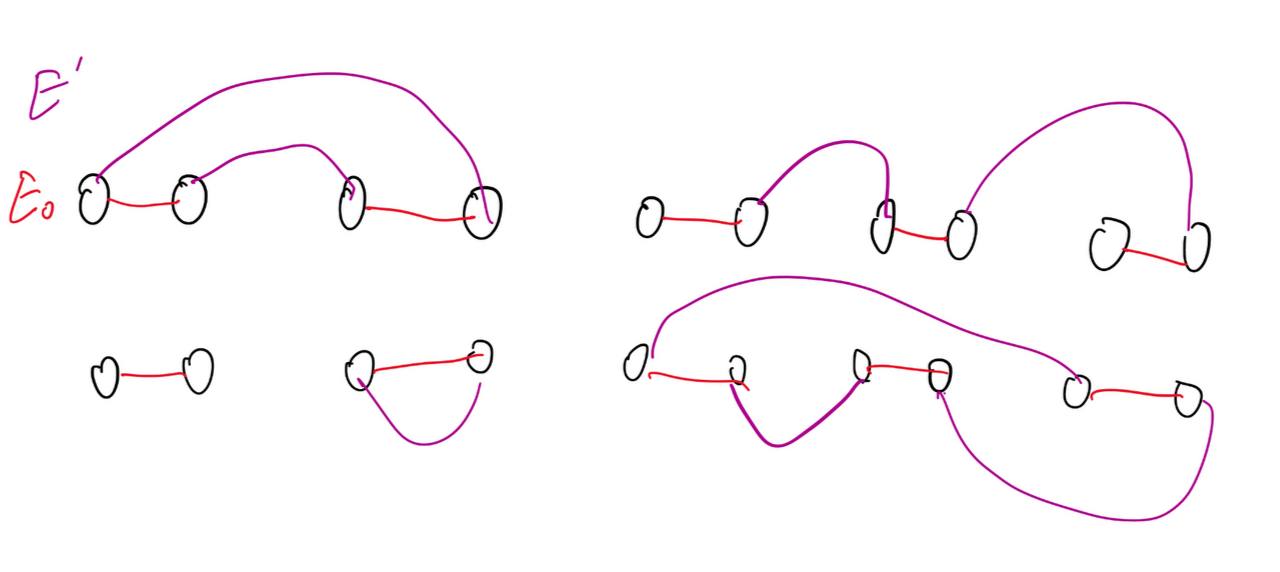
注意到由于 $2i-1$ 与 $2i$ 必须在同一个集合内,因此集合总数只有 $O(2^{n/2})$ 种。因此我们可以在 $O(2^{n/2} \cdot n^2)$ 的时间复杂度内计算出对所有 $S$ 将其划分成环/链的方案数。例如,对于链,我们可以记 $dp[mask][i]$ 表示已经经过的 block 的集合为 $mask$,现在位于点 $i$ 的贡献之和。对于环,我们可以直接枚举最大的点当作环的起点,由于 $\sum_{i\le n} 2^i = 2^{n+1}-1$,因此复杂度仍为 $O(2^{n/2} \cdot n^2)$。
划分完成后,我们可以使用 SOS DP(时间复杂度 $O(n \cdot 3^{n/2})$)或子集 exp(时间复杂度 $O(n^2 \cdot 2^{n/2})$)来计算最终将图划分成若干环/链的方案数。
总的时间复杂度为 $O(n \cdot 3^{n/2})$ 或 $O(n^2 \cdot 2^{n/2})$。由于常数上的差异,两种算法实际上均可通过。
